BTaRoT: Bayesian Tracking and Reasoning over Time
EPSRC Reference: EP/K020153/1
Start Date: April 2013
End Date: September 2016
Background -
Publications
Faculty
Postdocs
Background
The project aims to provide new advances in computational methods for reasoning about many objects that evolve in a scene over time. Information about such objects arrives, typically in a real-time data feed, from sensors such as radar, sonar, LIDAR and video. The new and exciting part of this project is in automated understanding of the `social interactions' that underlie a multi-object scene. The outcomes from this ambitious project could cause a paradigm shift in tracking methodology if successful, moving away from the traditional viewpoint of a scene in which objects move independently of one another, towards an integrated viewpoint where object interactions are automatically learned and used in improved decision-making processes. Applications include vehicle tracking, mapping, animal behaviour modelling, economic models and social network modelling.
These sophisticated and difficult problems can all be posed very elegantly using probability theory, and in particular using Bayesian theory. While generic and straightforward to pose, there are substantial challenges for our problem area in terms of how to pose the underlying prior models (what is a good way to model the random behaviour of networked objects in a scene?), and how do we carry out the very demanding computational calculations that are required for many-object scenes? These modelling and computational challenges form a major part of the project, and will require substantial new theoretical and applied algorithm development over the course of the project. We will develop novel computational methods based principally around Monte Carlo computing, in which very carefully designed randomised data are used to approximate very accurately the integrations and optimisations required in the Bayesian approach.
Publications
- J. Murphy and E. Ozkan and P. Bunch and S.J. Godsill, "Sparse Structure Inference for Group and Network Tracking", (forthcoming)
- J. Murphy and S.J. Godsill, "Sequential Sparse System Estimation for Linear Systems with Nonlinear Observations", (forthcoming)
- M.F. Ahmad, J. Murphy, D. Vatansever, E. Stamatakis, and S.J. Godsill, "Bayesian Inference of Task-Based Functional Brain Connectivity Using Markov Chain Monte Carlo Methods", (forthcoming)
- P. Bunch, J. Murphy and S.J. Godsill, "Annealed MCMC for Bayesian Learning of Linear Gaussian State Space Models with Changepoints", (forthcoming)
- P. Bunch, J. Murphy and S.J. Godsill, "Bayesian Learning of Degenerate Linear Gaussian State Space Models using Markov Chain Monte Carlo", IEEE Transactions on Signal Processing (accepted for publication), 2016
- J. Murphy and S.J. Godsill, "Bayesian Learning of Degenerate Linear Gaussian State Space Models using Markov Chain Monte Carlo", IEEE Journal of Selected Topics in Signal Processing 10(2) 328-342, 2016
- M.F. Ahmad, J. Murphy, D. Vatansever, E. Stamatakis, and S.J. Godsill, "Tracking changes in functional connectivity of brain networks from resting-state fMRI using particle filters", IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2015
- J. Murphy and S.J. Godsill, "Efficient filtering and sampling for a class of time-varying linear systems", IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2015
- F. Lindsten, M. I. Jordan and T. B. Schön "Particle Gibbs with Ancestor Sampling". Journal of Machine Learning Research (accepted for publication), 2014. (preprint available at [arXiv])
Background Material
- Bunch, P and Godsill, SJ (2013) _Particle Smoothing Algorithms for Variable Rate Models._ IEEE Transactions on Signal Processing, 61. pp. 1663-1675.
- Carmi, A and Septier, F and Godsill, SJ (2012) _The Gaussian mixture MCMC particle algorithm for dynamic cluster tracking._ Automatica, 48. pp. 2454-2467. ISSN 0005-1098.
- Pang, SK and Godsill, SJ and Li, J and Septier, F (2011) Sequential inference for dynamically evolving groups of objects.In: Inference and Learning in Dynamic Models. CUP.
- Pang, SK and Li, J and Godsill, SJ (2011) _Detection and Tracking of Coordinated Groups._ IEEE T AERO ELEC SYS, 47. pp. 472-502. ISSN 0018-9251
- Whiteley, NP and Singh, SS and Godsill, SJ (2010) _Auxiliary particle implementation of the probability hypothesis density filter._ IEEE Transactions on Aerospace and Electronic Systems, 46. pp. 1437-1454. ISSN 0018-9251
- Whiteley, NP and Johansen, AM and Godsill, SJ (2010) Monte Carlo filtering of piecewise deterministic processes.Journal of Computational and Graphical Statistics. pp. 1-21. ISSN 1061-8600
- S.J. Godsill, J. Vermaak, K-F. Ng, and J-F. Li. Models and algorithms for tracking of manoeuvring objects using variable rate particle filters. Proc. IEEE , May 2007.
- S.J. Godsill. Particle filters for continuous-time jump models in tracking applications. In ESAIM: PROCEEDINGS of Oxford Workshop on Particle Filtering , 2007.
Recent Work
Some recent project highlights have included work on the following topics:
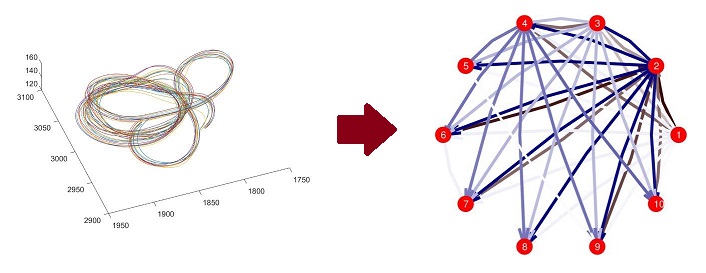
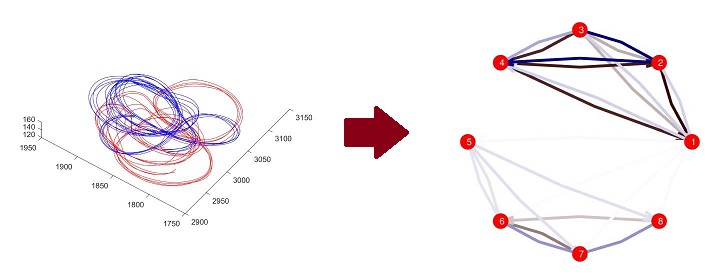
- Structure Learning for Tracking Data - By applying sparse structure learning methods to tracking problems, it is possible to learn about structure and relationships that exist between tracked objects. Applying such techniques to bird flocks such as the pigeon flocks pictured below, it is possible to start to learn about social relationships and networks of influence in these groups
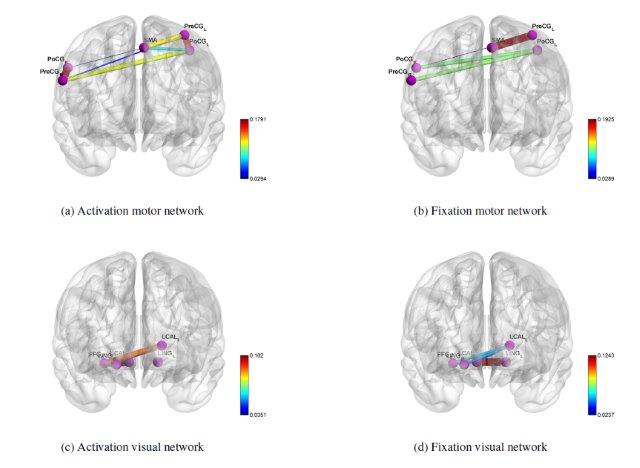
- Learning Functional Brain Networks - Sparse system inference methods can be used to learn about functional relationships in the brain, including (Granger) causality, giving insight into how human brains operate during tasks and in their resting state
- Particle MCMC Methods in High Dimensions - using blocking schemes it is possible to apply Particle Gibbs sampling to high dimensional systems, opening the possibility of using this powerful inference algorithm in high dimensional applications such as data assimilation
- Nonlinear Interaction Detection - detecting nonlinear relationships between tracked objects is a challenging problem, which can be tackled using nonparametric estimation approaches. For example, the nonlinear inter-object relationships in the system below are estimated from observation of the individual objects over time. Red lines show true inter-object relationships (with separation distance)
- Changepoint Detection and System Estimation in Linear Systems - changepoints in unknown linear systems are hard to detect using standard Monte Carlo approaches due to the strong local maxima in the posterior distribution. Using annealing methods it is possible to learn such systems using MCMC (where here red lines show true changepoint times and the histogram shows sampled changepoint times)
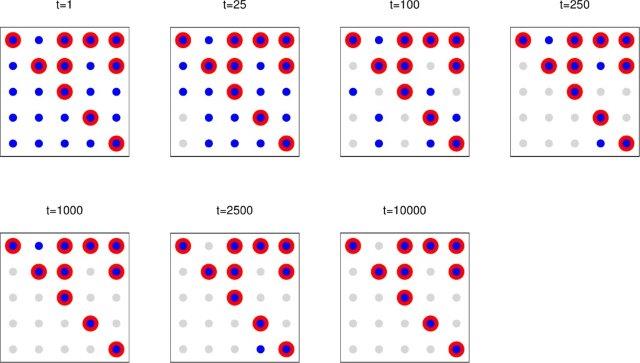
- Sparse Online Structure Inference - sparsity patterns in the relationships between elements of multivariate systems can be learned online using sequential Monte Carlo (SMC) approaches; in the figure below red dots indicate the true sparsity pattern and blue dots show the inferred sparsity pattern after a number of SMC steps